Aantal Bladeren:741 Auteur:Site Editor Publicatie tijd: 2024-08-30 Oorsprong:aangedreven
Het berekenen van de juiste vlakke patroonindeling is van cruciaal belang om een afgewerkt onderdeel van goede kwaliteit te krijgen druk op de rem. Toch hebben veel CAD- en CNC-programmeurs geen idee hoe ze de vereiste waarden moeten berekenen. Jaren geleden hebben de echte experts spiekbriefjes gemaakt en deze aan de muur geplakt. Ze leerden de nieuwe leerling alleen hoe hij de resultaten op het spiekbriefje moest toepassen, niet hoe hij de cijfers moest berekenen. Nu zijn die experts met pensioen en is het tijd voor een nieuwe generatie om de juiste manier te leren om de juiste vlakke patroonindeling te berekenen.
Het berekenen van de platte patroonlengte uit het 3D-onderdeel is echt niet zo moeilijk. Hoewel je misschien verschillende formules zult vinden die beweren dat bereken de buigtoeslag (Zie Buigdefinities), het is meestal dezelfde formule, alleen vereenvoudigd door de hoek of een K-factor in te vullen. Oh, en ja, je moet de K-factor kennen om de buigtoeslag te berekenen.

Laten we beginnen met een eenvoudige L-beugel. Op de afbeelding is te zien dat de poten van de beugel 2' en 3' zijn. De materiaaldikte is 0,125', de binnenradius is 0,250', en de buighoek is 90 graden. De platte lengte is het totaal van het platte gedeelte van beide flenzen plus de lengte door de boog van het bochtgebied. Maar bereken je dat aan de binnenkant van het materiaal of aan de buitenkant? Geen van beide! Dit is waar de K-factor een rol speelt. De K-factor is het percentage van de materiaaldikte waarbij er geen uitrekking of samendrukking van het materiaal plaatsvindt, bijvoorbeeld de neutrale as. Voor deze eenvoudige L-beugel gebruik ik een K-factor van 0,42.

De formule (zie Buigformules) is:
Buigtoeslag = Hoek * (π / 180) * (Straal + K-factor * Dikte).
Als we onze cijfers inpluggen, hebben we: Buigtoeslag = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475'
De lengte van het platte patroon is dus 1,625' + 2,625' + 0,475' wat gelijk is aan 4,725'. Dus als u de platte lengte van alle flenzen bij elkaar optelt en één buigtoeslag voor elk buiggebied optelt, krijgt u de juiste platte lengte van het onderdeel.
Maar kijk eens naar de tekening. Dat is niet de manier waarop wij normaal gesproken een plaatwerkonderdeel dimensioneren. De afmetingen gelden meestal voor het snijpunt van de flenzen of de mallijn. Dit betekent dat we voor elk buiggebied twee keer de materiaaldikte plus de buigradius (ook wel Setback genoemd) moeten aftrekken. Voor deze set afmetingen zou het eenvoudiger zijn om de buigcompensatiewaarde te berekenen. Met de waarde voor Buigcompensatie kunt u de lengte van elke flens optellen met behulp van de afmetingen van de vormlijn en vervolgens één Buigcompensatie per buiggebied aan het totaal toevoegen. Het is -0,275, een negatief getal, wat betekent dat u dit bedrag aftrekt van het totaal van de flenslengtes, 5', om 4,725' te krijgen.
Buigtoeslag = Hoek * (π / 180) * (Straal + K-factor * Dikte)
Buigcompensatie = Buigtoeslag – (2 * Set Back)
Binnen Set Back = bruin (Hoek / 2) * Radius Buiten
Terugzetten = bruin (hoek / 2) * (straal + dikte)

Buigtoeslag – De lengte van de boog door het bochtgebied op de neutrale as.
Buighoek – De ingesloten hoek van de boog gevormd door de buigbewerking.
Buigcompensatie – De mate waarin het materiaal wordt uitgerekt of samengedrukt door de buigbewerking. Er wordt aangenomen dat alle rek of compressie plaatsvindt in het buiggebied.
Buig lijnen – De rechte lijnen op de binnen- en buitenoppervlakken van het materiaal waar de flensgrens het bochtgebied ontmoet.
Binnen buigradius – De straal van de boog op het binnenoppervlak van het buiggebied.
K-factor – Definieert de locatie van de neutrale as. Het wordt gemeten als de afstand van de binnenkant van het materiaal tot de neutrale as gedeeld door de materiaaldikte.
Vorm lijnen – Voor bochten van minder dan 180 graden zijn de mallijnen de rechte lijnen waar de oppervlakken van de flens die het bochtgebied begrenzen elkaar kruisen. Dit gebeurt zowel aan de binnen- als aan de buitenkant van de bocht.
Neutrale as – Kijkend naar de dwarsdoorsnede van de bocht, is de neutrale as de theoretische locatie waar het materiaal niet wordt samengedrukt of uitgerekt.
Terugzetten - Bij bochten kleiner dan 180 graden is de set back de afstand van de buiglijnen tot de mallijn.
Voor zover ik weet bestaat er geen formule voor het berekenen van de k-factor. Oh, ik weet zeker dat een wiskundige ingenieur ergens een formule heeft. Maar het is waarschijnlijk te complex voor de meesten van ons om te begrijpen of te kunnen gebruiken.
De k-factor is het percentage van de materiaaldikte waarbij er geen uitrekking of samendrukking van het materiaal in het buiggebied plaatsvindt. De neutrale as dus!
Hoe harder het materiaal, hoe minder compressie er is aan de binnenkant van de bocht. Daarom wordt er meer uitgerekt aan de buitenkant en beweegt de neutrale as naar de binnenkant van de bocht. Zachtere materialen laten meer compressie aan de binnenkant toe en de neutrale as blijft dichter bij het midden van de materiaaldikte.
Buigradius heeft een soortgelijk effect. Hoe kleiner de buigradius, hoe meer compressie nodig is en de neutrale as beweegt naar de binnenkant van de bocht. Op een grotere straal. de neutrale as blijft nabij het midden van de materiaaldikte.

Om u te helpen de berekeningsformule van de ongevouwen buiglengte eenvoudiger en sneller onder de knie te krijgen, hebben we vier algemene coëfficiëntentabellen voor u op een rij gezet, zestien berekeningsformules van de ongevouwen buiglengte geïllustreerd, en we nemen ook enkele voorbeelden voor een beter begrip. Ik hoop dat de volgende inhoud u praktisch kan helpen. Als u vragen heeft, neem dan gerust contact met ons op.






A, B --- buiglengte van het werkstuk
P'---buigcoëfficiënt van randbuiging (buigfactor: één factor minus één buiging)
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgebreide lengte L=A+B-P', wat L=25+65-5,5=84,5 is
Volgens Tabel 1 is de plaatdikte 3, is de onderste matrijs V25 en is de buigcoëfficiënt 5,5
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.

A(A1), B --- buiglengte van het werkstuk
P'---buigcoëfficiënt van randbuiging (buigfactor: één factor minus één buiging)
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgebreide lengte L=A+T+B-2*P', wat L=50+2+50-2*3,4=95,2 is
Volgens Tabel 1 is de plaatdikte 2, is de onderste matrijs V12 en is de buigcoëfficiënt 3,4
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.

A(A1), B (B1) - buiglengte van het werkstuk
P'---buigcoëfficiënt van randbuiging (buigfactor: één factor minus één buiging)
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgebreide lengte L=A+T+B+T-3*P', wat L=50+2+90+2-3*3,4=133,8 is
Volgens Tabel 1 is de plaatdikte 2, is de onderste matrijs V12 en is de buigcoëfficiënt 3,4
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.

A, B (B1) - buiglengte van het werkstuk
P'---buigcoëfficiënt van randbuiging (buigfactor: één factor minus één buiging)
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgerekte lengte L=A+A+B+T+T-4*P', namelijk l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8
Volgens Tabel 1 is de plaatdikte 1,5, de onderste matrijs V12 en de buigcoëfficiënt 2,8
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.

A(A1), B (B1) - buiglengte van het werkstuk
P'---buigcoëfficiënt van randbuiging (buigfactor: één factor minus één buiging)
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgevouwen lengte L=A+T+A+T+B+B1+B1-6*P'
dat is l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2
Volgens Tabel 1 is de plaatdikte 1,5, de onderste matrijs V12 en de buigcoëfficiënt 2,8
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.

A, B --- buiglengte van het werkstuk
P'---afvlakkende buigcoëfficiënt van de filet
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgebreide lengte L=A+B-P', die L=25+65-1=89 is
Volgens Tabel 2 is de plaatdikte 2, is de onderste matrijs V12 en is de buigfactor de helft van de plaatdikte
Opmerking: Volgens Tabel 2 heeft de selectie van verschillende onderste matrijzen verschillende buigcoëfficiënten en verschillende plaatdiktes.
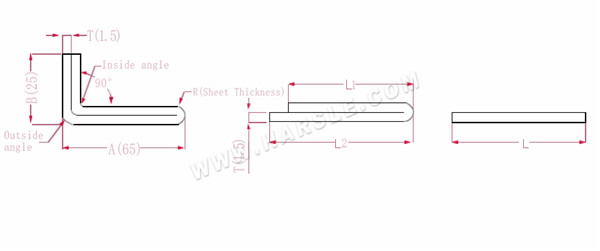
A, B --- buiglengte van het werkstuk
P1 --- buigcoëfficiënt van binnenhoek
P2 --- buigcoëfficiënt van externe buighoek
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgebreide lengte L1=(A-1,5) +(B-1,5)-P1, dat is L1= (65-1,5) +(25-1,5)-3,2=83,8
L2=A+B-P2, dat is L2=65+25-4,1=85,9
L=L1+L2-T/2, dat wil zeggen L=83,8+85,9-0,75=168,95
Volgens Tabel 2 is de plaatdikte 1,5, is de onderste matrijs V12, is de buigcoëfficiënt van de binnenhoek 3,2, is de buigcoëfficiënt van de buitenste hoek 4,1 en is de buigcoëfficiënt 180 0,75.
Opmerking: Volgens Tabel 2 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.
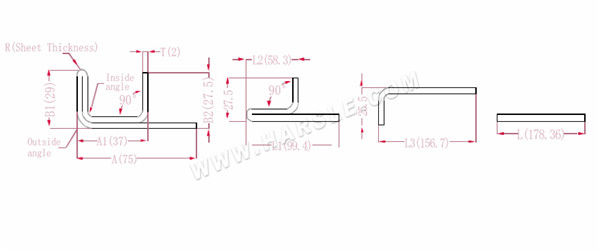
A, A1, A2, B1, B2, L, L1, L2, L3 --- buiglengte van werkstuk
P1 --- buigcoëfficiënt van binnenhoek
P2 --- buigcoëfficiënt van externe buighoek
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgebreide lengte L1=(A1-T) +(B2-T)-P1, wat L1= (35-2) +(34-2)-3,7=61,3 is
L2=(B1-T) +(A2-T)-P1, dat is L2= (50-2) +(34-2)-3,7=76,3
L3=A+B1+B2-2*P2, dat is L3=70+35+50-2*4,6+145,8
L=L1+L2+L3-2*P3, dat wil zeggen L=61,3+75,3+145,8-2*1=280,4
Volgens Tabel 2 is de plaatdikte 2, is de onderste matrijs V12, is de buigcoëfficiënt van de binnenhoek 3,7, is de buigcoëfficiënt van de buitenste hoek 4,6 en is de buigcoëfficiënt 90 1.
Opmerking: Volgens Tabel 2 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.
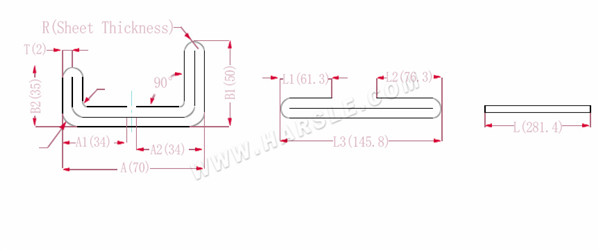
A, A1, A2, B1, B2, L, L1, L2, L3 --- buiglengte van werkstuk
P1 --- buigcoëfficiënt van binnenhoek
P2 --- buigcoëfficiënt van externe buighoek
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgebreide lengte L1=(A1-T) +(B2-T)-P1, wat L1= (35-2) +(34-2)-3,7=61,3 is
L2=(B1-T) +(A2-T)-P1, dat is L2= (50-2) +(34-2)-3,7=76,3
L3=A+B1+B2-2*P2, dat is L3=70+35+50-2*4,6+145,8
L=L1+L2+L3-2*P3, dat wil zeggen L=61,3+75,3+145,8-2*1=280,4
Volgens Tabel 2 is de plaatdikte 2, is de onderste matrijs V12, is de buigcoëfficiënt van de binnenhoek 3,7, is de buigcoëfficiënt van de buitenste hoek 4,6 en is de buigcoëfficiënt 90 1.
Opmerking: Volgens Tabel 2 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.
Diagram en berekeningsformule van stapbuigen
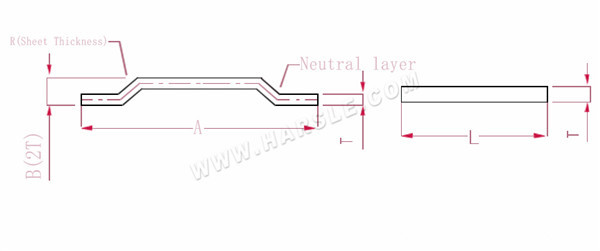
A, B --- buiglengte van het werkstuk
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
Uitgevouwen lengte L=A+1
Opmerking: Wanneer de stap gelijk is aan de dikte van twee platen, tel dan 0,5 op voor elke stap en 1 voor elke stap.
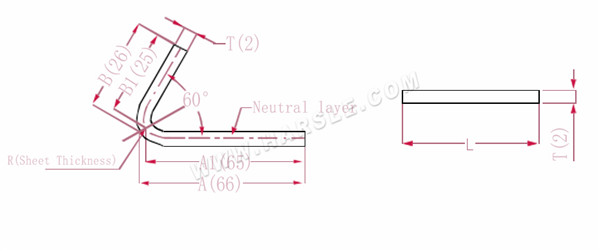
A(A1), B (B1) - buiglengte van het werkstuk
P'---buigcoëfficiënt van randbuiging (buigfactor: één factor minus één buiging)
R---bocht en filet (algemeen plaatdikte)
T --- materiaaldikte
De uitbreidingslengte L=(AT) +(BT)-P', wat L= (66-1) +(26-1)-2=65+25-2=88 is
Volgens Tabel 3 is de plaatdikte 2, is de onderste matrijs V12 en is de buigcoëfficiënt 60 2
Opmerking: Volgens Tabel 3 wordt de neutrale laag geselecteerd als de buiglengte en -breedte.
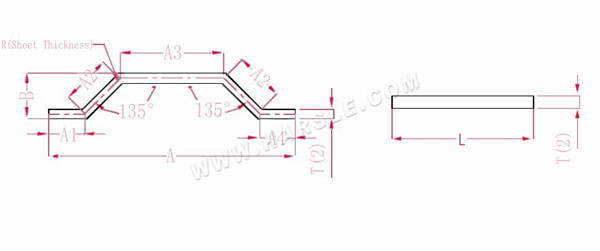
A (A1, A2, A3, A4), B --- buiglengte van het werkstuk
P --- buigfactor van 135 buighoeken
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
De uitgevouwen lengte L = A1+A2+A3+A2+A4-PP.
Let op: dezelfde drukstapbuiging hoeft slechts twee coëfficiënten te verminderen
Volgens Tabel 3: de plaatdikte is 2, de onderste matrijs is V12 en de buigcoëfficiënt bij 135 is 1,1.
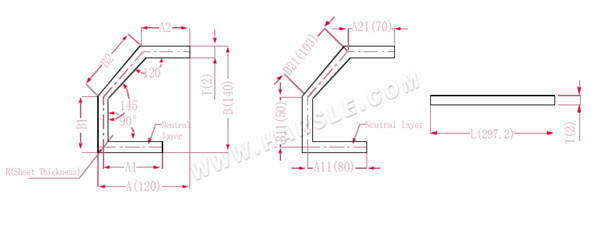
A (A1, A2), B (B1, B2) - buiglengte van het werkstuk
P1---120° buigcoëfficiënt
P2---145° buigcoëfficiënt
P3---90° buigcoëfficiënt
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
Opmerking: als de grafische grootte op de vorm is gemarkeerd, moet de vormgrootte worden geconverteerd naar de neutrale laaggrootte bij het berekenen van de uitvouwlengte;
De uitgevouwen lengte L=A11+B11+B21+A21-P1-P2-P3, dat wil zeggen l = 80+50+103+70-1,7-0,7-3,4 = 297,2
Volgens Tabel 3: de plaatdikte is 2, de onderste matrijs is V12, de 120 buigcoëfficiënt is 1,7, de 145 buigcoëfficiënt is 0,7 en de 90 buigcoëfficiënt is 3,4
Opmerking: Volgens Tabel 3 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.
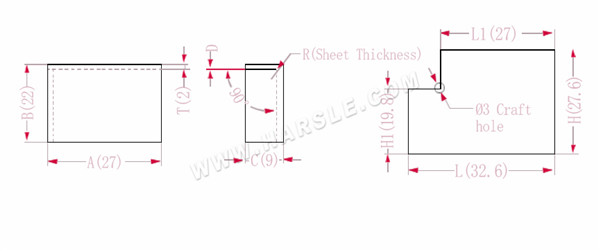
A, B, C --- lengte, breedte en hoogte van de buigrand van het werkstuk
P --- buigcoëfficiënt
R --- bocht en afronding (doorgaans plaatdikte)
H(H1), l (L1) - de uitgevouwen lengte van elke zijde
T --- materiaaldikte
D --- buigprocesspeling (doorgaans 0 ~ 0,5)
De uitgebreide lengte L1=A, wat L1=27 is
L=A+CP, dat wil zeggen L=27+9-3,4=32,6
H1=BTD, dat wil zeggen H1=22-2-0,2=19,8. Opmerking: D is 0,2.
H=B+CP, dat wil zeggen H=22+9-3,4=27,6
Volgens Tabel 1: de plaatdikte is 2, de onderste matrijs is V12 en de buigcoëfficiënt is 3,4
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.
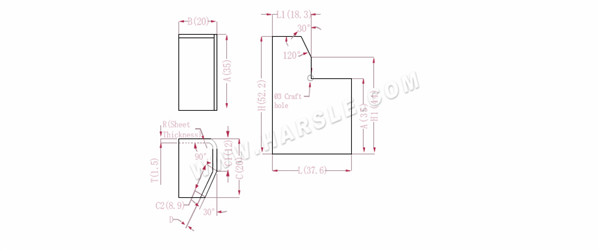
A, B, C --- lengte, breedte en hoogte van de buigrand van het werkstuk
H(H1), L (L1) - de uitgevouwen lengte van elke zijde
P---90° buigcoëfficiënt P1---30° buigcoëfficiënt
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
D --- buigprocesspeling (doorgaans 0 ~ 0,5)
De uitgebreide lengte L1=BTD, wat L1=20-1,5-0,2=18,3 is
L=B+C1+C2-P-P1, dat is L=20+12+8,9-2,8-0,5=37,6
H1=C1+APD, dat wil zeggen H1=12+35-2,8-0,2=44. Opmerking: D is 0,2.
H=A+CP, dat wil zeggen H=35+20-2,8=52,2
Volgens tabel 1: de plaatdikte is 1,5, de onderste matrijs is V12, de buigcoëfficiënt is 2,8 en de 30-buigcoëfficiënt is 0,5
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.

A, B, C --- lengte, breedte en hoogte van de buigrand van het werkstuk
H(H1), L (L1) - de uitgevouwen lengte van elke zijde
P --- buigcoëfficiënt
R --- bocht en afronding (doorgaans plaatdikte)
T --- materiaaldikte
D --- buigprocesspeling (doorgaans 0 ~ 0,5)
De uitgerekte lengte H1=B-B1-D, oftewel H1=50-12-0,3=37,7. Opmerking: D is 0,2.
H2=BTD, dat wil zeggen H2=50-2,5-0,3=47,2
H=B+C+B1-2*P, dat wil zeggen H=50+47+12-2*4,5=100
L1=A+CTDP, dat is L1=55+47-2,5-0,3-4,5=94,7
L=A+C+B2-2*P, dat is L=55+47+12-2*4,5=105
Volgens Tabel 1: de plaatdikte is 1,5, de onderste matrijs is V16 en de buigcoëfficiënt is 4,5
Opmerking: Volgens Tabel 1 zijn de verschillende buigcoëfficiënten van de onderste matrijzen en de verschillende plaatdiktes verschillend.